FFT – Transformée de Fourier rapide : principe et applications
Aujourd’hui, on va voir en détail ce qu’est la FFT, ou Transformée de Fourier rapide, un algorithme fondamental en traitement du signal et analyse fréquentielle.
Qu’est-ce que la FFT ?
La FFT est une méthode efficace pour calculer la Transformée de Fourier discrète (TFD) d’un signal. La TFD permet de décomposer un signal numérique en une somme de sinusoïdes de différentes fréquences, ce qui est essentiel pour analyser le contenu fréquentiel d’un signal.
Fft fft – fast fourier transform, qu\'est-ce que la fft & fft
Sans la FFT, le calcul direct de la TFD est coûteux en temps de calcul, avec une complexité en O(N²) pour un signal de N points. La FFT optimise ce processus en réduisant cette complexité à O(N log N), rendant l’analyse en temps réel possible dans de nombreuses applications électroniques.
Principe de la FFT
La FFT exploite la symétrie et la périodicité des racines de l’unité complexes pour diviser un problème TFD de taille N en sous-problèmes plus petits, généralement de taille N/2. Cette approche dite « diviser pour régner » est la clé de sa rapidité.
- Décomposition du signal d’entrée en deux sous-séquences : les échantillons pairs et impairs.
- Calcul récursif de la TFD de chaque sous-séquence.
- Combinaison des résultats avec des coefficients complexes appelés facteurs twiddle.
Cette décomposition récursive est répétée jusqu’à atteindre des séquences de taille 1, ce qui rend le calcul très rapide et structuré.
Applications de la FFT en électronique
La FFT est omniprésente en électronique, que ce soit pour l’analyse audio, la modulation numérique, le traitement d’images, ou encore le diagnostic des équipements. Elle permet notamment :
- De détecter les fréquences dominantes dans un signal capté (ex. : bruit, vibration).
- D’implémenter des filtres numériques en domaine fréquentiel.
- D’effectuer une analyse spectrale pour identifier des défauts dans un système électronique.
- D’améliorer la compression audio et vidéo par transformation des données.
Exemple simple de FFT
Considérons un signal discret de 8 échantillons :
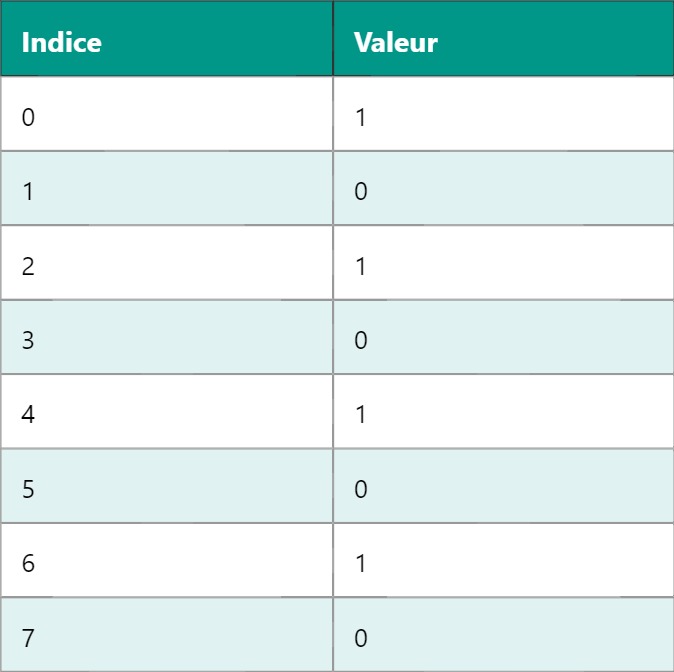
La FFT de ce signal mettra en évidence une fréquence fondamentale correspondant au motif répétitif du signal, avec un calcul rapide grâce à la décomposition en sous-séquences.
Optimisations et variantes
Plusieurs variantes de la FFT existent pour optimiser les calculs selon la nature des données ou des contraintes matérielles :
- FFT radix-2 : la plus classique, basée sur des tailles de données puissances de 2.
- FFT radix-4 : plus rapide sur certains matériels en regroupant 4 points à la fois.
- FFT en temps réel : adaptée aux systèmes embarqués pour un traitement continu.
Les microcontrôleurs modernes et FPGA intègrent souvent des modules matériels dédiés à la FFT pour accélérer les traitements.
La maîtrise de la FFT est essentielle pour tout ingénieur électronique travaillant sur le traitement du signal, la communication ou la mesure. Demain, nous pourrons approfondir le fonctionnement des filtres numériques, qui utilisent souvent la FFT pour optimiser leur réponse.